| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Spring
- roll over
- template/callback
- jwt-java
- monitoring
- ELK
- 화자분리
- API Gateway
- curl
- java
- metricbeat
- 자료구조
- supabase
- pyannote
- 파이썬
- kong
- umc
- elastic search
- C++
- 메소드
- 하이브리드 데이터 모델
- mybatis
- fosslight
- DI
- Nice
- devops
- prometeus
- konga
- docker
- OpenSource
- Today
- Total
youngseo's TECH blog
[BOJ|PYTHON] 백준 2618 경찰차 | 상황의 규칙성을 파악해 DP로 구현 본문
- 문제정리
https://www.acmicpc.net/problem/2618
2618번: 경찰차
첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 N(5 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 W(1 ≤ W ≤ 1,000)가 주어진다. 셋째 줄부터 (W+2)번째 줄
www.acmicpc.net
- 생각노트
두 자동차가 가는 길이 있다고 했을 때 어떻게 하면 최소로 갈 수 있을까.
이때 각 자동차를 "무조건 가까운 곳"으로 선택해서 가는 방법은 조금 생각해보면 안 된다는 것을 알 수 있다. 몇 번째 사건을 누가 처리하느냐에 따라 의존성이 계속해서 바뀌기 때문이다. (아무리 경찰차2랑 현재 거리에서는 가깝다고 하더라도 경찰차1이 사건 1,2,3을 처리하다가 더 가까워질 수 있음)
그럼 이 사건의 의존성이 어떻게 벌어지는지를 예제케이스 + 테스트케이스 로 파악해 보자.
상황을 잘 관찰해보면,
만약 경찰차 A가 3, 경찰차 B가 4 상황에 있다면 -> 그 전 상황은 다음 케이스 모두 된다.
1. A가 3에 있고 B가 2에 있었다.
2. A가 3에 있고 B가 1에 있었다.
3. A가 3에 있고 B가 0에 있었다.
만약 경찰차 A가 3, 경찰차 B가 5 상황에 있다면 -> 그 전 상황은 다음 케이스 뿐이다.
1. A가 3에 있고 B가 4에 있었다.이렇게 상황의 규칙성을 파악한 후 DP로, 즉 작은 문제에서부터 큰 문제로 확장해 나갈 수 있다.(Bottom up 방식)
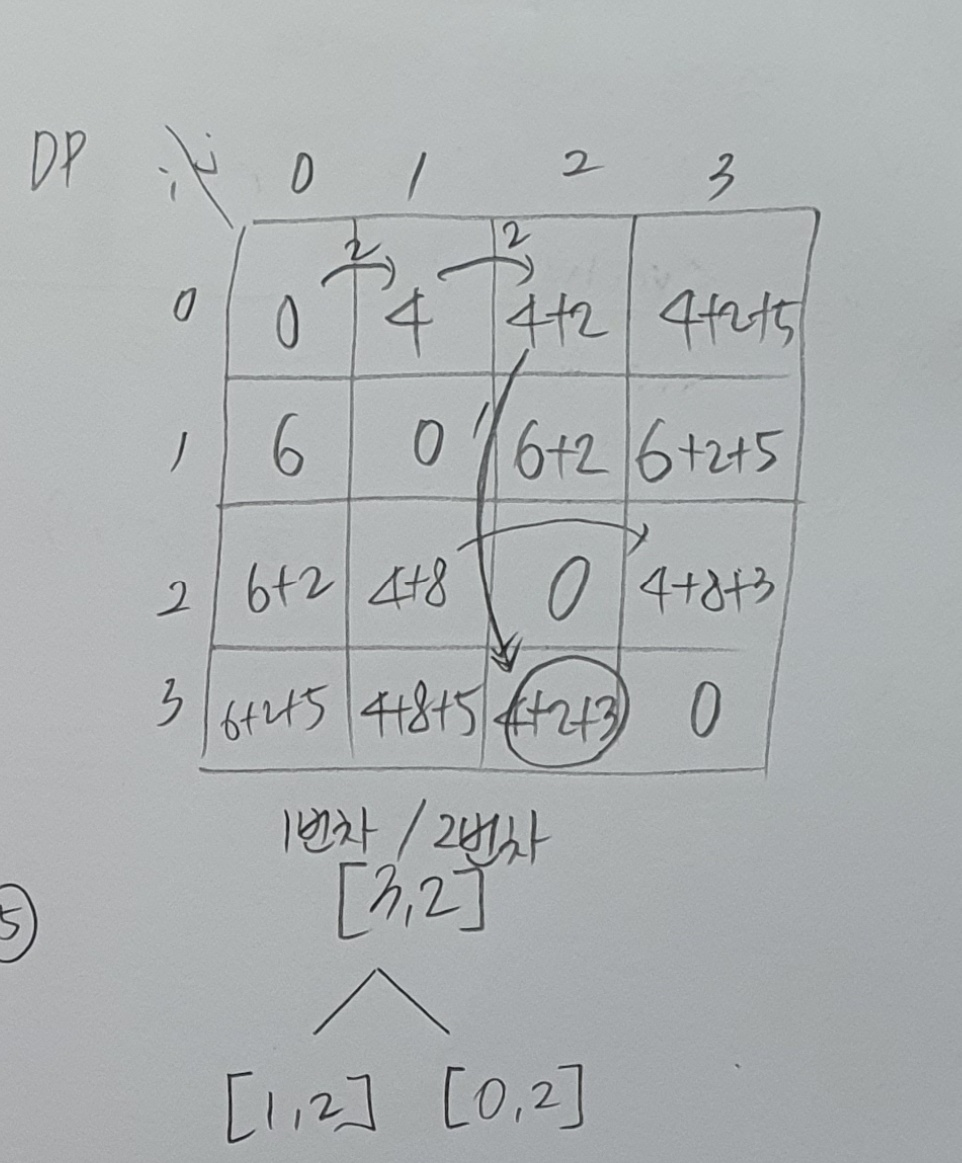
- 구현방법 선택
DP
- 코드화
import sys
input=sys.stdin.readline
N=int(input())
W=int(input())
position=[[0,0]]
position1=[[N-1 ,N-1]]
for _ in range(W):
i,j=map(int,input().split())
position.append([i-1,j-1])
position1.append([i-1,j-1])
dp=[[float('inf') for _ in range(W+1)] for _ in range(W+1)]
dp_trace=[[0 for _ in range(W+1)] for _ in range(W+1)] #어디에서 왔니
#print(position)
dp[0][0]=0
ans=[]
#O(W^3)
for i in range(W+1):
for j in range(W+1):
if i==j: continue
if i<j:
if i and j-1==i:
for k in range(j-1):
if dp[i][j]>dp[i][k]+abs(position1[j][0]-position1[k][0])+abs(position1[j][1]-position1[k][1]):
dp[i][j]=dp[i][k]+abs(position1[j][0]-position1[k][0])+abs(position1[j][1]-position1[k][1])
dp_trace[i][j]=k
else:
dp[i][j]=dp[i][j-1]+abs(position1[j][0]-position1[j-1][0])+abs(position1[j][1]-position1[j-1][1])
dp_trace[i][j]=j-1
else:
if j and i-1==j:
for k in range(i-1):
if dp[i][j]>dp[k][j]+abs(position[i][0]-position[k][0])+abs(position[i][1]-position[k][1]):
dp[i][j]=dp[k][j]+abs(position[i][0]-position[k][0])+abs(position[i][1]-position[k][1])
dp_trace[i][j]=k
else:
dp[i][j]=dp[i-1][j]+abs(position[i][0]-position[i-1][0])+abs(position[i][1]-position[i-1][1])
dp_trace[i][j]=i-1
# for i in dp:
# print(*i)
compare=float('inf')
I,J=0,0
#O(W^2)
for i in range(W):
if dp[i][W]<compare: I,J = i,W; compare=dp[i][W]
if dp[W][i]<compare: I,J = W,i; compare= dp[W][i]
# print('I랑 J',I,J)
# print(dp_trace)
print(dp[I][J])
for i in range(W):
if J>I:
J=dp_trace[I][J]
ans.append(2)
else:
I=dp_trace[I][J]
ans.append(1)
for i in range(W-1,-1,-1):
print(ans[i])
#역추적??- 주의해야할 것들
2차원배열로 구현할 수 있음을 파악한 후에는 DP의 행, 열을 뭘로 채택해서 툴로 써야할지 고민하면 좋을 것 같다.
(시간초과와도 관계 있을 수 있으므로 크기까지 고려!)
'알고리즘 > 세부구현' 카테고리의 다른 글
| [BOJ|PYTHON]백준 17501 - 그래프 표현하는 독특한 방법 +D/BFS (0) | 2022.09.11 |
|---|---|
| [BOJ|PYTHON]백준 20046 - 다익스트라 (3) | 2022.09.11 |
| [BOJ|PYTHON]외판원의 순환 DP(top down과 bottom up) (0) | 2022.08.21 |
| [BOJ|python]백준 1562 비트마스킹 (+DP) (0) | 2022.08.12 |
| [BOJ|PYTHON] 15684 사다리조작 (0) | 2022.08.06 |

