목차
1. 문제 정리
2. 알고리즘 증명 및 설명
3. 코드 구현
2261번: 가장 가까운 두 점
첫째 줄에 자연수 n(2 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 줄에는 차례로 각 점의 x, y좌표가 주어진다. 각각의 좌표는 절댓값이 10,000을 넘지 않는 정수이다. 여러 점이 같은 좌표를 가질 수도
www.acmicpc.net
1. 문제정리
2차원 평면 위에 여러 점들이 콕콕 박혀 있다.
이 점들 사이 거리 중 가장 짧은 거리를 찾으려 한다.

2. 알고리즘 증명 및 설명
일단 일일이 다 해보는 전략에 따르면, 모든 가능한 점의 쌍 거리를 구하는 데 O(N^2), 정렬하는 데 O(N^2 logN)으로 총 O(N^2 logN)의 시간복잡도가 걸린다.
그럼 이 2차원 평면을 두 개로 쪼개서 해결해보자.

위와 같은 상태에서 세 가지 경우에서 가장 짧은 거리가 나올 수 있다.
- 왼쪽에 있는 점들 사이에서 가장 짧은 거리 -> PL
- 오른쪽에 있는 점들 사이에서 가장 짧은 거리 ->PR
- 왼쪽에서 한 점, 오른쪽에서 한 점을 고른 점 사이 가장 짧은 거리
세 번째 경우가 가장 까다로우므로 일단 첫번째, 두번째 경우에서 나온 가장 짧은 거리가 각각 P1, P2로 나왔다고 하자.
그 중 P1이 더 짧은 애가 나왔다. min(P1,P2)=P1
이를 이용해 우리는 세번째 경우를 더 좁힐 수 있다.

위와 같이 거리가 P1 이하인 점들로 후보군이 좁혀진다.
하지만 항상 극단적인 상태로 반증을 시도해볼 필요가 있다.
아래와 같이 쪼로록 줄을 선다면 결국 우리는 모든 가능한 점의 쌍을 구하는 방법과 같아지게 되어 O(N^2 logN)의 상황을 맞닥뜨린다.
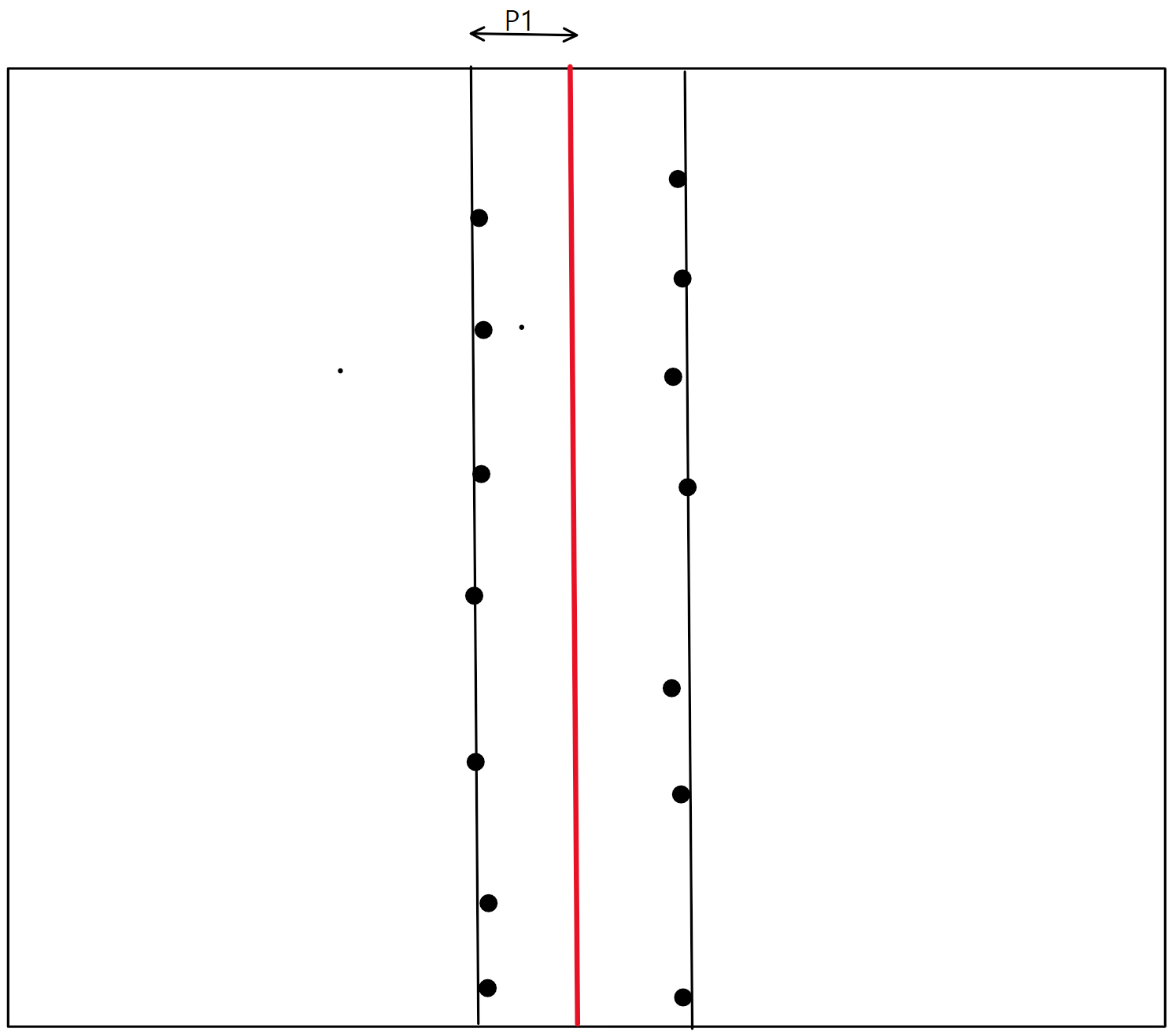
하지만 이 상황에서 좀 더 생각해보면, 어차피 오른쪽 점들 사이의 거리들은 P1보다 작다! 그래서 가장 극단적인 경우에 점이 아무리 몰려 있다고 해도 아래와 같은 상황이 가장 극단적이다. 따라서 우리는 점 하나당 비교를 4번만 하면 된다!!

따라서 T(N)=2T(N/2)+O(N) (N/2*4개의 점) 즉, O(NlogN)의 시간복잡도를 가지고 해결할 수 있다.
3. 코드 구현
출처는 다음과 같다. 문제풀이보단 문제 공부에 가까웠다..
import sys, random
input = sys.stdin.readline
n = int(input())
pl = [list(map(int,input().split())) for i in range(n)]
# x축 기준 정렬
pl.sort(key=lambda x: x[0])
# 두 점 사이의 거리 계산 함수
def getDist(p1, p2):
return (p1[0] - p2[0])**2 + (p1[1] - p2[1])**2
def dac(start,end):
# 점 하나의 거리는 없으니 최대값 리턴
if start == end:
return float('inf')
# 점이 두 개 남으면 사이의 거리 리턴
if end - start == 1:
return getDist(pl[start],pl[end])
# 분할정복 실행
mid = (start + end)//2
minDist = min(dac(start, mid), dac(mid,end))
# x축 기준으로 후보 점들을 찾는다.
target_pl = []
for i in range(start, end+1):
if (pl[mid][0] - pl[i][0])**2 < minDist:
target_pl.append(pl[i])
# y축 기준 정렬
target_pl.sort(key=lambda x: x[1])
# y축 기준으로 후보 점들 사이의 거리 비교
t = len(target_pl)
for i in range(t-1):
for j in range(i+1,t):
if (target_pl[i][1] - target_pl[j][1])**2 < minDist:
minDist = min(minDist, getDist(target_pl[i],target_pl[j]))
else:
break
# 현재 후보 점이 다음 점과 최소 거리보다 멀다면 더 볼 필요가 없음.
# 위 처리가 없으면 시간 초과 발생
return minDist
print(dac(0,n-1))
'알고리즘 > 세부구현' 카테고리의 다른 글
| [PS | 한 번에 맞자!] 백준 3048 (0) | 2023.07.10 |
|---|---|
| [PS | 한번에 맞자!] 백준 21278 (0) | 2023.07.10 |
| [BOJ|PYTHON]백준20047 - DP TOPDOWN (0) | 2022.09.11 |
| [BOJ|PYTHON]백준 17501 - 그래프 표현하는 독특한 방법 +D/BFS (0) | 2022.09.11 |
| [BOJ|PYTHON]백준 20046 - 다익스트라 (3) | 2022.09.11 |
